Dưới đây là bài viết về: Đề thi giữa học kì 1 môn Toán 9 năm 2023 - 2024 có đáp án cung cấp cho học sinh những chủ đề chính cần nắm vững và ôn tập để chuẩn bị tốt cho kỳ thi giữa học kì 1.
Mục lục bài viết
1. Đề cương ôn thi giữa học kì 1 môn Toán 9 năm 2023 – 2024:
Dưới đây là đề cương ôn thi giữa học kì 1 môn Toán lớp 9 với các chủ đề chi tiết:
PHẦN ĐẠI SỐ
Chủ đề 1: Căn bậc hai và căn bậc ba
– Định nghĩa căn bậc hai là một số thực dương sao cho bình phương của nó bằng một số thực cho trước. Căn bậc ba là một số thực sao cho lập phương của nó bằng một số thực cho trước.
– Các tính chất của căn bậc hai và căn bậc ba, ví dụ như căn bậc hai của một số dương duy nhất, căn bậc hai của một số âm không tồn tại trong tập số thực, căn bậc ba của một số âm.
– Cách tính giá trị của căn bậc hai và căn bậc ba, ví dụ như sử dụng phương pháp khai phương để tính căn thức bậc hai, hoặc phương pháp rút gọn đa thức để tính căn thức bậc ba.
– Bài toán liên quan đến căn bậc hai và căn bậc ba, ví dụ như giải phương trình có chứa căn thức bậc hai hoặc căn thức bậc ba.
Chủ đề 2: Căn thức bậc hai và hằng đẳng thức
– Công thức nhẩm căn thức bậc hai, ví dụ như căn bậc hai của một biểu thức đơn giản như a^2, a^2 + 2ab + b^2, a^2 – 2ab + b^2.
– Công thức khai phương để tìm nghiệm của phương trình bậc hai, ví dụ như phương pháp sử dụng khai phương để giải phương trình ax^2 + bx + c = 0.
– Công thức hằng đẳng thức liên quan đến căn thức bậc hai, ví dụ như hằng đẳng thức khai phương: (a + b)^2 = a^2 + 2ab + b^2.
Chủ đề 3: Khai phương
– Định nghĩa khai phương là phương pháp giải phương trình bậc hai bằng cách đưa phương trình về dạng (a + b)^2 = c hoặc (a – b)^2 = c.
– Cách khai phương để giải phương trình bậc hai, bậc ba, ví dụ như phương pháp sử dụng khai phương để giải phương trình bậc hai ax^2 + bx + c = 0 hoặc phương trình bậc ba ax^3 + bx^2 + cx + d = 0.
– Đặc điểm và ứng dụng của khai phương trong giải các bài toán thực tế.
Chủ đề 4: Biến đổi, rút gọn biểu thức
– Các phép biến đổi biểu thức đơn giản, ví dụ như nhân đôi, bình phương, phân đôi, phân thức đồng dạng, phép chia đa thức cho một đa thức đơn giản.
– Công thức rút gọn đa thức đơn giản, ví dụ như rút gọn đa thức bậc hai, bậc ba, bậc ba với nhiều biến.
– Cách áp dụng biến đổi và rút gọn biểu thức trong giải các bài toán tính toán, ví dụ như tìm giá trị của biểu thức trong một phép tính cụ thể, giải phương trình hoặc bất phương trình đơn giản.
PHẦN HÌNH HỌC
Chủ đề 5: Hệ thức về cạnh và đường cao
– Hệ thức định nghĩa cạnh, đường cao và các hệ thức liên quan, ví dụ như định nghĩa cạnh kề, cạnh đối, đường cao từ một đỉnh.
– Cách tính giá trị của cạnh, đường cao trong tam giác, dựa trên các hệ thức liên quan, ví dụ như định lý Pythagoras, định lý đường cao, định lý nhân tính.
– Bài toán liên quan đến cạnh và đường cao của tam giác, ví dụ như tính diện tích tam giác, tính chu vi tam giác, xác định đỉnh của tam giác dựa trên các giá trị cạnh và đường cao.
Chủ đề 6: Tỉ số lượng giác
– Định nghĩa tỉ số lượng giác của một góc trong tam giác vuông, bao gồm sin, cos, tan, cotan, sec, và cosec.
– Công thức tính tỉ số lượng giác dựa trên các giá trị của cạnh trong tam giác vuông, ví dụ như cách tính sin, cos, tan của một góc dựa trên giá trị cạnh kề, cạnh đối.
– Cách áp dụng tỉ số lượng giác trong giải các bài toán thực tế, ví dụ như tính độ dốc của một dốc, tính chiều cao của một tòa nhà, giải các bài toán liên quan đến đo đạc và định vị trong không gian, tính khoảng cách, diện tích, thể tích của các hình học đa diện dựa trên các tỉ số lượng giác.
Chủ đề 7: Hệ thức về cạnh và góc
– Định nghĩa và tính chất của các hệ thức về cạnh và góc trong tam giác không vuông, bao gồm định lý giữa, định lý cô-sin, định lý tích, định lý cosin, định lý phụ.
– Cách áp dụng các hệ thức về cạnh và góc để giải các bài toán liên quan đến tam giác không vuông, ví dụ như tính các góc trong tam giác, tính độ dài cạnh, tính diện tích tam giác.
– Bài toán liên quan đến tính chất của cạnh và góc trong các hình học không gian, ví dụ như tính thể tích của khối chóp, khối cầu, khối trụ dựa trên các hệ thức về cạnh và góc.
Đây là một đề cương ôn tập giữa học kì 1 môn Toán lớp 9, cung cấp cho học sinh những chủ đề chính cần nắm vững và ôn tập để chuẩn bị tốt cho kỳ thi giữa học kì 1. Học sinh cần chú ý nắm vững các kiến thức cơ bản, hiểu rõ các công thức, định lý, và cách áp dụng chúng vào giải các bài toán. Ngoài ra, cần luyện tập thường xuyên, giải nhiều bài tập thực hành để rèn luyện kỹ năng và nâng cao năng lực giải quyết các bài toán Toán học.
2. Đề thi giữa học kì 1 môn Toán 9 năm 2023 – 2024 có đáp án:
Bài 1 (2,0 điểm).
1. Thực hiện phép tính.

2. Tìm điều kiện của x để các biểu thức sau có nghĩa:

Bài 2 (2,0 điểm).
1. Phân tích đa thức thành nhân tử.

Bài 4 (3,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết BC = 8cm, BH = 2cm.
a. Tính độ dài các đoạn thẳng AB, AC, AH.
b. Trên cạnh AC lấy điểm K (K ≠ A, K ≠ C), gọi D là hình chiếu của A trên BK. Chứng minh rằng: BD.BK = BH.BC.
c. Chứng minh rằng: ![]()
Bài 5 (0,5 điểm).
Cho biểu thức P = x3 + y3 – 3(x + y) + 1993. Tính giá trị biểu thức P với:

Đáp án và Hướng dẫn làm bài
Bài 1.
1. Thực hiện phép tính

2. Tìm điều kiện của x để biểu thức có nghĩa

Bài 2.
1. Phân tích đa thức thành nhân tử:

2. Giải phương trình

⇔ x + 1 = 25 ⇔ x = 24 (thỏa mãn điều kiện xác định)
Vậ
Bài 3.
a. Rút gọn biểu thức
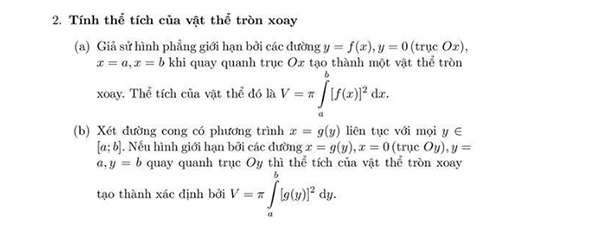

Bài 4.

a.
Ta có ΔABC vuông tại A, đường cao AH
⇒ AB2 = BH.BC = 2.8 = 16 (hệ thức lượng trong tam giác vuông)
⇒ AB = 4cm (Vì AB > 0)
Mà BC2 = AB2 + AC2 (Định lý Pitago trong tam giác vuông ABC)
![]()
Có HB + HC = BC ⇒ HC = BC – HB = 8 – 2 = 6 cm
Mà AH2 = BH.CH = 2.6 = 12 (hệ thức lượng trong tam giác vuông)
⇒ ![]() (Vì AH > 0)
(Vì AH > 0)
b.
Ta có ΔABK vuông tại A có đường cao AD
⇒ AB2 = BD.BK (1)
Mà AB2 = BH.BC (chứng minh câu a) (2)
Từ (1) và (2) suy ra BD.BK = BH.BC
c.
Bài 5.

3. Ma trận đề thi giữa học kì 1 môn Toán 9 năm 2023 – 2024 có đáp án:
Chủ đề
Mức độ | Nhận biết | Thông hiểu | Vận dụng | Vận dụng cao | Tổng | |||||||
TN | TL | TN | TL | TN | TL | TN | TL | Số câu Điểm, Tỉ lệ | TN | TL | ||
PHẦN ĐẠI SỐ | ||||||||||||
Chủ đề 1: Căn bậc hai Căn bậc ba |
Câu 8 |
Câu 12 |
Câu 13 |
|
|
|
| |||||
Số câu | 1,0 |
| 1,0 |
| 1,0 |
|
| 3,0 | 3,0 |
| ||
Số điểm | 0,2 |
| 0,2 |
| 0,2 |
|
| 0,6 | 0,6 |
| ||
Tỉ lệ % | 2,0 |
| 2,0 |
| 2,0 |
|
| 6,0 | 6,0 |
| ||
Chủ đề 2: Căn thức bậc hai và hằng đẳng thức |
Câu 9 |
Câu 15 |
Câu 14 Câu 21a Câu 22a
|
Câu 24 |
|
|
| |||||
Số câu | 1,0 |
| 1,0 |
| 1,0 | 2,0 |
| 1,0 | 6,0 | 3,0 | 3,0 | |
Số điểm | 0,2 |
| 0,2 |
| 0,2 | 1,0 |
| 1,0 | 2,6 | 0,6 | 2,0 | |
Tỉ lệ % | 2,0 |
| 2,0 |
| 2,0 | 10,0 |
| 10,0 | 26,0 | 6,0 | 20,0 | |
Chủ đề 3: Khai phương |
Câu 2
| Câu 2 Câu 20 Câu 10 |
Câu 21b
|
|
|
|
| |||||
Số câu | 1,0 |
| 3,0 |
|
| 1,0 |
| 5,0 | 4,0 | 1,0 | ||
Số điểm | 0,2 |
| 0,6 |
|
| 0,5 |
| 1,3 | 0,8 | 0,5 | ||
Tỉ lệ % | 2,0 |
| 6,0 |
|
| 5,0 |
| 13,0 | 8,0 | 5,0 | ||
Chủ đề 4: Biến đổi, rút gọn biểu thức |
|
Câu 17 Câu 19
|
Câu 11 Câu 1
|
Câu 4
|
|
|
| |||||
Số câu |
| 2,0 |
| 2,0 |
| 1,0 |
| 5,0 | 5,0 |
| ||
Số điểm |
| 0,4 |
| 0,4 |
| 0,2 |
| 1,0 | 1,0 |
| ||
Tỉ lệ % |
| 4,0 |
| 4,0 |
| 2,0 |
| 10,0 | 10,0 |
| ||
PHẦN HÌNH HỌC | ||||||||||||
Chủ đề 5: Hệ thức về cạnh và đường cao |
Câu 5
|
Câu 6 | Câu 16 Câu 22b
| Câu 23a Câu 23b |
|
|
| |||||
Số câu | 1,0 |
| 1,0 |
| 1,0 | 1,0 |
| 2,0 | 6,0 | 3,0 | 3,0 | |
Số điểm | 0,2 |
| 0,2 |
| 0,2 | 0,5 |
| 1,5 | 2,1 | 0,6 | 2,0 | |
Tỉ lệ % | 2,0 |
| 2,0 |
| 2,0 | 5,0 |
| 15,0 | 26,0 | 6,0 | 20,0 | |
Chủ đề 6: Tỉ số lượng giác |
|
Câu 3 |
Câu 21c |
|
|
|
| |||||
Số câu |
| 1,0 |
|
| 1,0 |
| 2,0 | 1,0 | 1,0 | |||
Số điểm |
| 0,2 |
|
| 0,5 |
| 0,7 | 0,2 | 0,5 | |||
Tỉ lệ % |
| 2,0 |
|
| 5,0 |
| 7,0 | 2,0 | 5,0 | |||
Chủ đề 7: Hệ thức về cạnh và góc |
| Hình vẽ Câu 23 |
| Câu 7 Câu 23c |
|
|
| |||||
Số câu |
|
| 0,0 |
| 1,0 | 1,0 | 2,0 | 1,0 | 1,0 | |||
Số điểm |
|
| 0,25 |
| 0,2 | 0,75 | 1,2 | 0,2 | 1,0 | |||
Tỉ lệ % |
|
| 2,5 |
| 2,0 | 7,5 | 9,5 | 2,0 | 10,0 | |||
Tổng câu | 4,0 |
| 9,0 | 0,0 | 5,0 | 5,0 | 2,0 | 4,0 | 29,0 | 20,0 | 9,0 | |
Tổng điểm | 0,8 |
| 1,8 | 0,25 | 1,0 | 2,5 | 0,4 | 3,25 | 10,0 | 4,0 | 6,0 | |
Tỉ lệ % | 8,0 | 20,5 | 35,0 | 36,5 | 100,0 | 40,0 | 60,0 | |||||
BẢNG MÔ TẢ:
Chủ đề | Câu | Mức độ | Mô tả |
I. TRẮC NGHIỆM KHÁCH QUAN (4,0 điểm) | |||
Chủ đề 1: Căn bậc hai Căn bậc ba | Câu 8 | 1 | Nhận biết được số âm không có căn bậc hai số học. |
Câu 12 | 2 | So sánh được các biểu thức chứa căn bậc hai. | |
Câu 13 | 1 | Thực hiện được phép tính chứa căn bậc ba. | |
Chủ đề 2: Căn thức bậc hai và hằng đẳng thức | Câu 9 | 1 | Tìm được điều kiện xác định của biểu thức chứa căn thức bậc hai. |
Câu 15 | 1 | Khai căn được biểu thức chứa căn thức bậc hai. | |
Câu 14 | 2 | Tìm được giá trị của thỏa mãn đề bài. | |
Chủ đề 3: Khai phương | Câu 18 | 1 | Áp dụng được quy tắc khai phương và khai căn để thực hiện phép tính. |
Câu 2 | 1 | Áp dụng được quy tắc khai phương để thực hiện phép tính. | |
Câu 20 | 3 | Áp dụng được quy tắc khai phương để tìm nghiệm của phương trình. | |
Câu 10 | 4 | Áp dụng phân tích thành nhân tử. | |
Chủ đề 4: Biến đổi, rút gọn biểu thức | Câu 17 | 2 | Đưa được thừa số ra ngoài rồi thu gọn kèm điều kiện. |
Câu 11 | 2 | Vận dụng được hằng đảng thức để tính kèm điều kiện. | |
Câu 19 | 2 | Khử mẫu được biểu thức lấy căn. | |
Câu 1 | 2 | Trục căn thức dưới mẫu của biểu thức. | |
Câu 4 | 4 | Áp dụng các quy tắc để tìm được giá trị của thỏa mãn đề bài. | |
Chủ đề 5: Hệ thức về cạnh và đường cao | Câu 5 | 1 | Nhận biết được các định lý về các hệ thức về cạnh và đường cao trong tam giác vuông. |
Câu 16 | 2 | Áp dụng được hệ thức để tìm đường cao. | |
Câu 6 | 2 | Áp dụng được hệ thức để tìm cạnh huyền. | |
Chủ đề 6: Tỉ số lượng giác | Câu 3 | 2 | Áp dụng được công thức để tính được tan của một góc. |
Chủ đề 7: Hệ thức về cạnh và góc | Câu 7 | 3 | Áp dụng được các hệ thức về cạnh và góc để vận dụng vào bài toán thực tế. |
II. TỰ LUẬN: (6,0 điểm) | |||
Chủ đề 2: Căn thức bậc hai và hằng đẳng thức | Câu 21a | 2 | Áp dụng rút gọn biểu thức. |
Câu 22a | 2 | Áp dụng tìm | |
Câu 24 | 4 | Áp dụng các công thức và biến đổi để chứng minh đẳng thức. | |
Chủ đề 3: Khai phương | Câu 21b | 2 | Áp dụng quy tắc khai phương để rút gọn biểu thức. |
Chủ đề 6: Tỉ số lượng giác | Câu 21c | 2 | Áp dụng các tỉ số lượng giác để rút gọn biểu thức. |
Chủ đề 5: Hệ thức về cạnh và đường cao | Câu 22b | 2 | Áp dụng các hệ thức về cạnh và đường cao trong tam giác vuông để tìm |
Câu 23a | 2 | Áp dụng các hệ thức về cạnh và đường cao trong tam giác vuông để tính độ dài các đoạn thẳng | |
Câu 23b | 2 | Áp dụng các hệ thức về cạnh và đường cao trong tam giác vuông để chứng minh hệ thức. | |
Chủ đề 7: Hệ thức về cạnh và góc | Câu 23c | 4 | Áp dụng các hệ thức về cạnh và góc trong tam giác vuông để chứng minh hệ thức. |




