Tập hợp không chỉ là một khái niệm trong toán học mà còn là ứng dụng rất hữu ích trong thực tế. Hãy tham khảo bài viết dưới đây về tập hợp và các phép tính của tập hợp.
Mục lục bài viết
1. Khái niệm tập hợp là gì?
Tập hợp là một khái niệm toán học cơ bản (nhưng không thể định nghĩa cụ thể). Các tập hợp sẽ được kí hiệu bằng những chữ cái in hoa như A, B, C, D…,N, X, Y. Trong đó các phần tử của tập hợp cũng thường được kí hiệu bằng các chữ in thường như a, b, c, d, e…, n, x, y.
Vậy phần tử của tập hợp là gì?
Kí hiệu a ∈ A có nghĩa là a là một phần tử của tập hợp A hay là phân tử a thuộc tập hợp A. Ngược lại a∉ A để chỉ a không thuộc A, a không phải là một phần tử của tập hợp A.
Một tập hợp được thể hiện bằng cách liệt kê tất cả các phần tử của nó hoặc được chỉ được nêu ra bằng cách nhắc đến các tính chất đặc trưng của các phân tử trong tập hợp.
Ví dụ về tập hợp như: A = {1, -1} hay A = { x ∊ R/ x² +2 = 3 }
Và một tập hợp mà không có bất kì phân tử nào sẽ được gọi là tập hợp rỗng, với kí hiệu Ø.
2. Các kí hiệu và các loại tập hơn:
Tập hợp bao gồm các số tự nhiên được quy ước với kí hiệu là N
N={0, 2, 4, 6, 8, 10, 12..}
Tập hợp của các số nguyên được quy ước kí hiệu là Z
Z={…-5, -3, -1, 0, 1, 3, 5 …}
Tập hợp các số nguyên bao gồm các phân tử là các số tự nhiên và số đối của các số tự nhiên.
Trong khi đó tập hợp các số nguyên dương được kí hiệu là N*
N*={ 1, 3, 5, 7, 9, 11,13,…}
Tập hợp các số hữu tỉ được quy ước kí hiệu là Q
Q={ a/b; a, b∈Z, b≠0}
Một số hữu tỉ còn có thể biểu diễn bằng một số thập phân hữu hạn hoặc một số thập phân vô hạn tuần hoàn.
Tập hợp các số thực được quy ước kí hiệu là R
Mỗi số được biểu diễn bằng một số thập phân vô hạn không tuần hoàn và còn được gọi là một số vô tỉ. Tập hợp các số vô tỉ được quy ước kí hiệu là I. Tập hợp của các số thực bao gồm các số hữu tỉ và các số vô tỉ.
Các tập hợp con thường gặp nhất của tập hợp số thực:
Kí hiệu –∞ được đọc là âm vô cực (hoặc là âm vô cùng), kí hiệu +∞ được đọc là dương vô cực (hoặc là dương vô cùng).
Mối quan hệ các tập hợp số:
Ta sẽ có được: R = Q ∪ I
Các tập N ; Z ; Q ; R.
Quan hệ bao hàm giữa các tập hợp số sẽ được trình bày như sau : N ⊂ Z ⊂ Q ⊂ R
Mối quan hệ giữa các tập hợp số sẽ được thể hiện rõ nhất qua biểu đồ Ven. Sơ đồ Venn là một sơ đồ logic cho thấy mối quan hệ có thể có giữa các tập hợp hữu hạn khác nhau. Sơ đồ Venn có thể được biểu diễn như sau.
Tập hợp con
Vậy tập hợp con là gì? Ta có thể gọi A là tập hợp con của B, và được kí hiệu là A ⊂ B khi và chỉ khi x ∈ A suy ra x ∈ B
Hai tập hợp bằng nhau:
Tập hợp A và tập hợp B được gọi là hai tập hợp bằng nhau khi tất cả các phần tử của hai tập hợp đều như nhau và kí hiệu là A = B
A = B khi và chỉ khi A ⊂ B và B ⊂ A.
3. Các phép toán tập hợp:
Phép toán tập hợp là một khái niệm tương tự như phép toán cơ bản trên các số. Các tập hợp trong toán học có thể là một tập hợp hữu hạn các đối tượng, có thể là số, bảng chữ cái hoặc bất kỳ đối tượng nào trong thế giới thực. Đôi khi một nhu cầu phát sinh trong đó chúng ta cần thiết lập mối quan hệ giữa hai hoặc nhiều tập hợp. Các phép toán tập hợp là các phép toán được áp dụng trên hai hoặc nhiều tập hợp để phát triển mối quan hệ giữa chúng.
Có bốn phép toán tập hợp chính bao gồm phép hợp, phép giao, phép hiệu và phép lấy phần bù.
3.1. Phép hợp:
Với hai tập hợp A và B đã cho, A∪B (đọc là A hợp B) là tập hợp các phần tử phân biệt thuộc tập hợp A và tập hợp B hoặc cả hai. Số phần tử trong A ∪ B được cho bởi n(A∪B) = n(A) + n(B) − n(A∩B), trong đó n(X) là số phần tử của tập hợp X. Để Để hiểu rõ hơn về hoạt động tập hợp này , chúng ta hãy xem xét một ví dụ: Nếu A = {1, 2, 3, 4} và B = {4, 5, 6, 7}, thì hợp của A và B là cho bởi A ∪ B = {1, 2, 3, 4, 5, 6, 7}.
3.2. Phép giao:
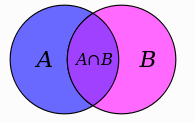
Cho hai tập hợp A và B đã cho, A∩B (đọc là A giao B) là tập hợp gồm các phần tử chung thuộc hai tập hợp A và B. Số phần tử của A∩B được cho bởi n(A∩B) = n(A)+n(B)−n(A∪B), trong đó n(X) là số phần tử trong tập hợp X. Để hiểu rõ hơn hoạt động tập hợp này của giao các tập hợp, chúng ta hãy xem xét một ví dụ: Nếu A = {1, 2, 3, 4} và B = {3, 4, 5, 7} thì giao điểm của A và B là A ∩ B = {3, 4}.
3.3. Phép hiệu:
Sự khác biệt hoạt động tập hợp giữa các tập hợp trừ các phần tử khỏi một tập hợp tương tự như khái niệm về sự khác biệt giữa các số. Hiệu giữa tập hợp A và tập hợp B được ký hiệu là A ∖ B liệt kê tất cả các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B. Để hiểu rõ hơn về hoạt động của tập hợp này, chúng ta hãy xem xét một ví dụ: Nếu A = {1, 2, 3, 4} và B = {3, 4, 5, 7}, thì hiệu giữa tập hợp A và B là A ∖ B = {1, 2}.
3.4. Phép lấy phần bù:
Cho A là tập con của tập E. Phần bù của A trong X là X∖A, ký hiệu là CxA là tập hợp cả các phần tử của E mà không là phần tử của A.. Để hiểu hoạt động tập hợp này của phần bù của các tập hợp tốt hơn, chúng ta hãy xem xét một ví dụ: Cho tập A={2;3;4},B={1;2} thì CAB =A∖B={3;4}
4. Thuộc tính của phép toán tập hợp:
Tính chất của phép toán tập hợp tương tự như tính chất của phép toán cơ bản trên số. Các thuộc tính quan trọng trên các hoạt động thiết lập được nêu dưới đây:
Luật giao hoán: Đối với hai tập hợp A và B bất kỳ, tính chất giao hoán được định nghĩa là:
A ∪ B = B ∪ A
Điều này có nghĩa là phép toán tập hợp của phép hợp hai tập hợp là giao hoán.
A ∩ B = B ∩ A
Điều này có nghĩa là phép toán tập hợp giao của hai tập hợp là giao hoán.
Luật kết hợp– Đối với ba tập hợp đã cho bất kỳ A, B và C, tính chất kết hợp được định nghĩa là,
(A ∪ B) ∪ C = A ∪ (B ∪ C)
Điều này có nghĩa là phép toán tập hợp của phép hợp các tập hợp là phép toán kết hợp.
(A ∩ B) ∩ C = A ∩ (B ∩ C)
Điều này có nghĩa là phép toán tập hợp giao của các tập hợp là phép toán kết hợp.
Định luật De-Morgan– Định luật De Morgan phát biểu rằng đối với hai tập hợp A và B bất kỳ, chúng ta có (A ∪ B)’ = A’ ∩ B’ và (A ∩ B)’ = A’ ∪ B’
– A ∪ A = A
– A ∩ A = A
– A ∩ ∅ = ∅
– A ∪ ∅ = A
– A ∩ B ⊆ A
– A ⊆ A ∪ B
Lưu ý quan trọng về hoạt động Set
Công thức lập phép toán cho hợp các tập hợp là n(A∪B) = n(A) + n(B) − n(A∩B) và công thức phép toán lập cho giao của các tập hợp là n(A∩B) = n(A )+n(B)−n(A∪B).
Hợp của bất kỳ tập hợp nào với tập hợp phổ biến sẽ tạo ra tập hợp phổ biến và giao của bất kỳ tập hợp A nào với tập hợp phổ biến sẽ tạo ra tập hợp A.
Hợp, giao, hiệu và bù là các phép toán khác nhau trên tập hợp.
Phần bù của tập phổ quát là tập rỗng U′ = ϕ. Phần bù của tập rỗng là tập phổ quát ϕ′ = U.
5. Một số bài tập có lời giải:
Ví dụ 1: Trong một trường học, mọi học sinh đều chơi bóng đá hoặc bóng bàn hoặc cả hai. Người ta thấy rằng 200 học sinh chơi bóng đá, 150 học sinh chơi bóng bàn và 100 học sinh chơi cả hai. Tìm xem có bao nhiêu sinh viên trong trường bằng cách sử dụng công thức Phép toán tập hợp.
Giải: Gọi số học sinh chơi bóng đá là n(F) và số học sinh chơi bóng bàn là n(S). Ta có n(F) = 200, n(S) = 150 và n(F ∩ S) = 100. Ta biết rằng,
n(F∪S) = n(F) + n(S) − n(F∩S)
Do đó, n(F∪S)=(200+150)−100
n(F∪S) = 350 − 100 = 250
Trả lời: Vậy tổng số học sinh toàn trường là 250 em.
Ví dụ 2:
Ví dụ 3:
Nếu A = {a, b, c, d, e}, B = {a, e, i, o, u}, U = {a, b, c, d, e, f, g, h ,i,j,k,l,o,u}. Thực hiện các phép toán sau trên tập hợp và tìm giải pháp.
a) A hợp B (A ∪ B)
b) A giao B (A ∩ B)
c)Phần bù của tập hợp A (A’)
d) A trừ B
Giải: a) A ∪ B = {a, b, c, d, e, i, o, u}
b) A ∩ B = {a, e}
c) A’ = {f, g, h, i, j, k, l, o, u}
d) A – B = {b, c, d}
Như vậy, một tập hợp là một tập hợp các phần tử. Một số ví dụ thực tế về các tập hợp là danh sách tất cả các tiểu bang trong một quốc gia, danh sách tất cả các hình dạng trong hình học , danh sách tất cả các số nguyên từ 1 đến 100. Chúng ta có thể xác định các vùng chung bằng cách sử dụng thao tác tập hợp giao điểm.




